A los futboleros nos encanta comparar jugadores. Es lo que vamos a hacer aquí con dos de los goleadores de la liga española. Por un lado, Kylian Mbappé, jugador del Real Madrid de 26 años y con un valor de mercado de 180 millones de euros. Por el otro, Ante Budimir, delantero de Osasuna de 33 años, con un valor de mercado de 5 millones de euros. A los futboleros nos encanta comparar jugadores. Es lo que vamos a hacer aquí con dos de los goleadores de la liga española. Por un lado, Kylian Mbappé, jugador del Real Madrid de 26 años y con un valor de mercado de 180 millones de euros. Por el otro, Ante Budimir, delantero de Osasuna de 33 años, con un valor de mercado de 5 millones de euros.
A los futboleros nos encanta comparar jugadores. Es lo que vamos a hacer aquí con dos de los goleadores de la liga española. Por un lado, Kylian Mbappé, jugador del Real Madrid de 26 años y con un valor de mercado de 180 millones de euros. Por el otro, Ante Budimir, delantero de Osasuna de 33 años, con un valor de mercado de 5 millones de euros.
En estas comparaciones solemos utilizar más el corazón que otra cosa y casi siempre acabamos defendiendo posiciones que benefician a nuestro equipo. Pero el fútbol cuenta en la actualidad con métricas establecidas que nos permiten argumentar y afirmar muy convencidos: “lo dicen los datos”.
En concreto, una nueva forma de medir la eficiencia de los goleadores consiste en comparar sus percentiles (goles conseguidos) en el contexto de la distribución probabilística de sus ocasiones (goles esperados, xG).
Pero ¿qué son los goles esperados? Está establecido que el valor xG de un penalti en las principales ligas europeas es 0.79, lo cual determina que la probabilidad de conseguir un gol es equivalente a lanzar un dado de 100 caras (zocchiedro) y obtener un número entre el 1 y el 79. Fallarlo será por tanto obtener un número entre el 80 y el 100, es decir, 21 posibilidades de cada 100, 0.21.
En la actualidad, los goles esperados de un equipo se calculan sumando los valores xG de todos sus tiros. De este modo se obtienen sus valores medios o esperanzas con dos decimales. Estos valores se comparan con los goles conseguidos, que son números enteros, para concluir qué equipo ha tenido más suerte o acierto.
Pues bien, utilizando la misma métrica podemos intercambiar (virtualmente) jugadores entre equipos. Si elegimos a Kylian Mbappé y Ante Budimir, primer y tercer goleador de la actual liga española, podemos agrupar sus tiros y sus xG correspondientes para calcular las probabilidades individuales de cada número de goles. Así podremos comparar goles (esperados) con goles (conseguidos) en sus mismas unidades.
Este valor nos dará la eficiencia de cada uno, que transportaremos a las ocasiones del otro para poder responder a la pregunta que da título a este artículo. Pero no con valores medios, como se hace habitualmente, sino cada uno con la distribución de sus ocasiones.
Calculamos la probabilidad de que los tiros registrados en la competencia se conviertan en un número determinado de goles (0, 1, 2…). Con dos ocasiones parece sencillo y se calcula muy fácil, pero si el número aumenta, ya es más complicado.
Por ejemplo, si tenemos 5 tiros, la probabilidad de meter 3 tiene que combinar todos los tiros en grupos de 3 acertados y 2 fallados, lo cual crece muy notablemente. En el caso que nos ocupa, tenemos 161 tiros de uno y 99 del otro, lo que hace el problema intratable si necesitamos calcular todas las combinaciones y calcular sus resultados.
Para poder manejarlo computacionalmente utilizamos el concepto de convolución. De forma resumida, se van computando los tiros sucesivamente. Por cada tiro, el número de goles potenciales aumenta en uno y las probabilidades calculadas hasta el momento se modifican según si el tiro que estamos añadiendo es gol o no.
La función de probabilidad acumulada asigna un valor a su rango percentil, que consiste en una medida de posición que divide una distribución en 100 partes iguales, indicando el porcentaje de datos que se encuentran por debajo de ese valor.
A partir del total de 161 tiros lanzados por Kylian Mbappé, resulta muy improbable conseguir 161 goles, pero no imposible. Por tanto su probabilidad no es cero. Lo mismo sucede con los 99 tiros de Budimir. Obtenemos por cada número de goles posibles su probabilidad, que se va acumulando de tal forma que el percentil de Mbappé respecto de su distribución de goles se obtiene sumando las probabilidades de conseguir desde 0 hasta sus 31 goles. Esto nos da un valor de 0.91. Por tanto, establecemos el percentil 91.
Para Budimir lo hacemos con sus 21 goles resultando un valor de 0.83, percentil 83. Podemos concluir por tanto que la eficiencia de ambos es muy alta pero con diferencias que traduciremos en goles intercambiando los escenarios.
El gráfico muestra los goles conseguidos y sus probabilidades. Vemos que la campana de Budimir es más picuda que la de Mbappé y que ésta es más ancha en la base, debido a que el primero presenta menos dispersión en la calidad de sus ocasiones.
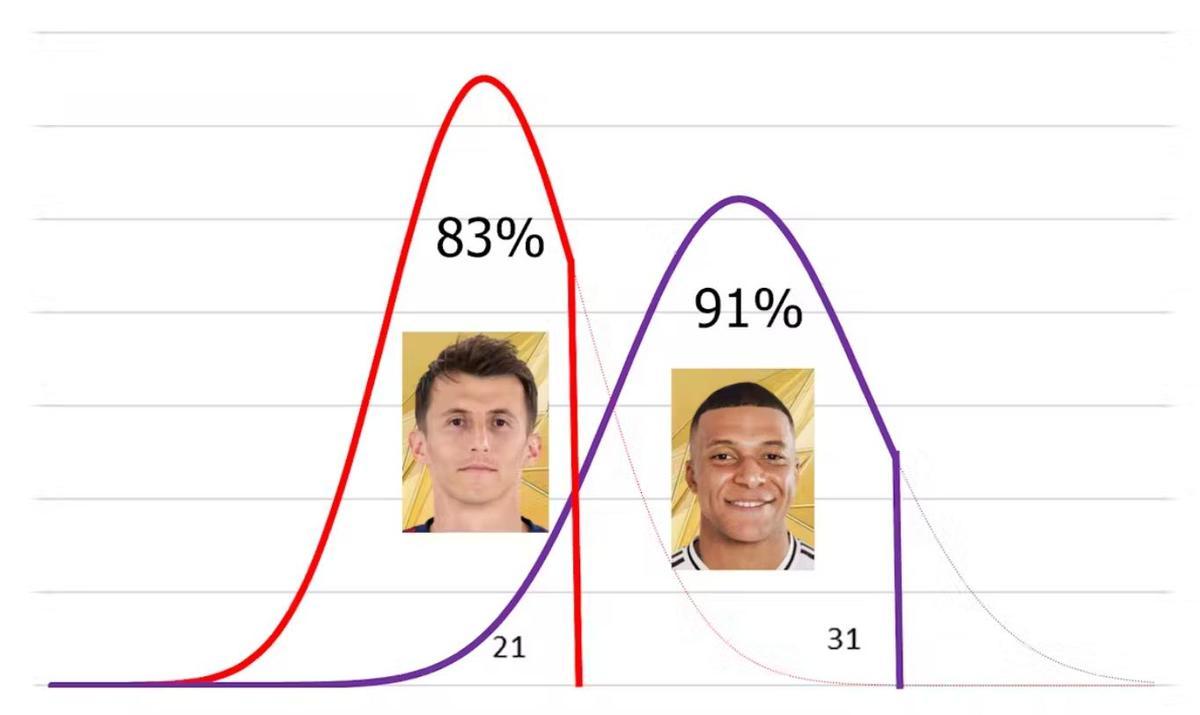
Atendiendo a esto, si el francés hubiera jugado en Osasuna habría conseguido un gol adicional, 22 (21). Si el croata hubiera vestido de blanco habría conseguido dos goles menos, 29 (31). Este cálculo intercambiado lo hacemos en sentido inverso, viendo cuántos goles cubren los percentiles de cada jugador en la distribución de las ocasiones del otro.
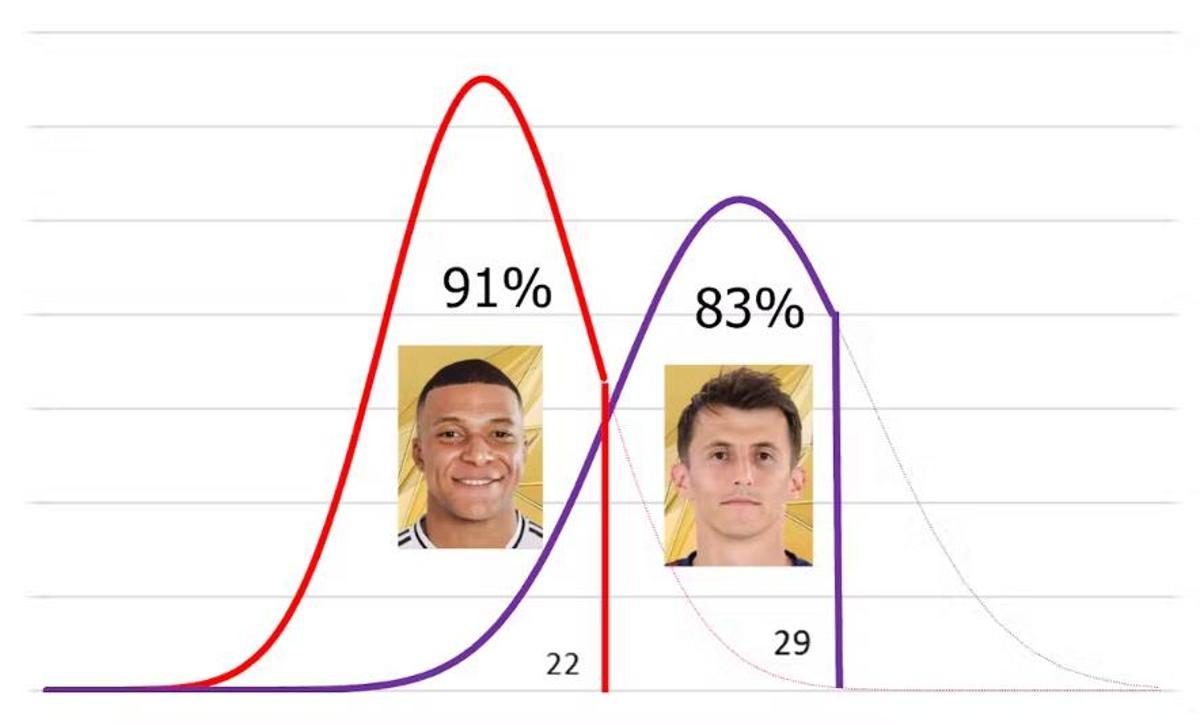
Aunque hay aspectos en la valoración de futbolistas que no estamos considerando, al menos hemos conseguido vestir a Mbappé de rojillo y a Budimir de merengue, evaluando lo más importante del desempeño de sus posiciones: los goles.
Tan solo dos goles distancian el desempeño de ambos si los hubiéramos intercambiado. Hay rumores que apuntan a que el croata puede vestir de blanco la próxima temporada. Nuestro estudio ha adelantado cuántos goles habría conseguido en caso de haberlo hecho durante la concluida temporada.
Si fuéramos el director deportivo del club, no podríamos desaconsejar su contratación. Su eficiencia es alta y promete seguir siéndolo en próximas temporadas, ya sea de “rojillo” o con otra camiseta.
Diario de Mallorca – Deportes




